A different approach to Convolution

When it comes to algorithms, performance is the first non functional requirement that comes into mind. Besides efficiency of the algorithm itself (complexity, branches, multiplications,…), there are a lot of things that can be done during implementation. Some optimizations might lead to higher code complexity, reduced readability and overall decreased maintainability. In this article we’ll take a different approach to implement the convolution algorithm in C/C++. It should be fast (enough) while being as maintainable as possible.

It is important to note that we’ll focus on small to mid-sized kernels from about 10 to 200 samples and therefore use the “classic” Convolution algorithm. Very small kernel sizes might benefit from Winograd’s minimal filtering algorithms, whilst large kernel sizes benefit from using FFT (Fast Fourier Transform).

Interesting for

This article is especially interesting if you

• are looking for an easy, maintainable and yet fast Convolution implementation in C++
• want to learn how to use online tools to try, test and benchmark C++ code
• want to get started with the process of optimizing algorithms for speed
• are looking for thoughts on maintainability and how it relates to performance
• want to explore how Convolution responds to simple input signals

Table of Contents

1. Convolution
   1. What is Convolution?
   2. How to Calculate Convolution?
   3. Direct Implementation
   4. Direct Implementation Optimized
2. Fast Feedback
   1. Online Benchmark
   2. Online Compiler
   3. Compiler Options for Vectorization
   4. Unit Testing
3. Optimization for Speed and Maintainability
   1. Reevaluate the Algorithm
      1. Experiment with Simple Input Signals
      2. Implementing the Transposed Structure
      3. Performance of the Transposed Structure
      4. Compiler Output of the Transposed Structure
      5. Optimize for Microsoft Visual Studio (MSVC)
   2. Cache Efficiency
      1. Measure Loop Order
   3. Most Efficient and Maintainable Implementation
      1. Features
      2. Further Speed Potential
4. Source Code
5. References

Convolution

What is Convolution?

There are a lot of good online articles about Convolution. Here are two i’d recommend:

• Intuitive Guide to Convolution [1] from Kalid Azad explains the math with many examples.
• The Convolution Series [2] from Jan Wilczek demonstrates how to implement Convolution.

How to Calculate Convolution?

The following equation shows the discrete Convolution for a finite kernel \(h\) with M values:

\[(x * h)[n] = \sum_{k=0}^{M} x[n-k]h[k]\]

For the implementation this means:

• \(x\) is an array of floating point values representing the input samples.
• \(h\) is an array of floating point values representing the kernel.
• The so called “kernel” is in terms of a filter it’s impulse response (=coefficients).
• It will take two loops to iterate over index \(n\) for \(x\) and index \(k\) for \(h\).
• Array indices must not be negative. When index \(n-k\) is negative, zero is used as value.

Direct Implementation

Following the equation and the directly derived requirements leads us to an implementation like this:

void directlyDerivedFromEquation(
    const float *const input, 
    const int inputLength, 
    const float *const kernel, 
    const int kernelLength, 
    float *const output)
{
    auto const outSize = inputLength + kernelLength - 1;
    for (auto outIndex = 0; outIndex < outSize; ++outIndex)
    {
        for (auto inputIndex = 0; inputIndex < inputLength; ++inputIndex)
        {
            auto const kernelIndex = outIndex - inputIndex;
            if ((kernelIndex >= 0) && (kernelIndex < kernelLength)) {
                output[outIndex] += (input[inputIndex] * kernel[kernelIndex]);
            }
        }
    }
}

To anticipate the results from Online Benchmark, the implementation above is more than 30 times slower than most others. From here we will have a look at how this can be optimized.

Direct Implementation Optimized

The first optimization attempt is to get the if statement (branch) out of the inner loop. These statements can prevent compiler optimizations. If at least the inner loop can get optimized, there should be a measurable improvement in performance. Branchless Programming [6] goes into much more detail on how branches affect the compiled result and how they can be replaced or optimized.

In this case the idea is to limit the inner loop to only iterate over the valid range of the arrays. The following implementation shows how this can be achieved:

void directlyDerivedFromEquationWithIfInOuterLoop(
    const float *const input, 
    const int inputLength, 
    const float *const kernel, 
    const int kernelLength, 
    float *const output)
{
  const auto outSize = inputLength + kernelLength - 1;
  for (auto outIndex = 0; outIndex < outSize; ++outIndex)
  {
    const auto outIndexPlusOne = outIndex + 1;
    const auto inputMin = (outIndexPlusOne >= kernelLength)? outIndexPlusOne - (kernelLength) : 0;
    const auto inputMax = (outIndexPlusOne < inputLength)? outIndexPlusOne: inputLength;
    for (auto inputIndex = inputMin; inputIndex < inputMax; ++inputIndex)
    {
      const auto kernelIndex = outIndex - inputIndex;
      output[outIndex] += (input[inputIndex] * kernel[kernelIndex]);
    }
  }
}

Fast Feedback

As ever: Strive for fast feedback. Measurement is key for performance optimization. We’ll have a look at tools that give us immediate results on how a piece of code performs, what the compiler is able to optimize and if the results are correct.

Online Benchmark

A great tool to compare the performance of different implementations is Quick C++ Benchmark [7]. We use it to compare the direct and the optimized implementation. This is the result:

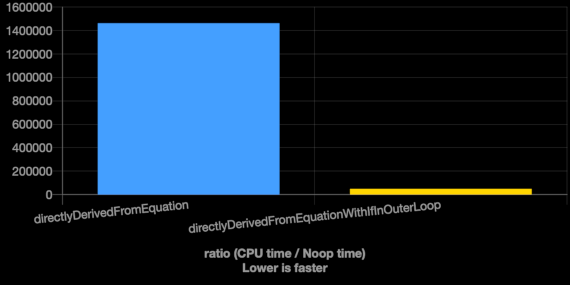
As mentioned earlier, the optimized implementation is about 30 times faster.

Benchmark Code

#include <vector>
#include <random>

std::vector<float> randomNumbers(int n, float min, float max)
{
    std::vector<float> vectorWithRandomNumbers(n);
    std::random_device randomDevice;
    std::mt19937 gen(randomDevice());
    std::uniform_real_distribution<float> distribution(min, max);
    for (float &value : vectorWithRandomNumbers)
    {
        value = distribution(gen);
    }
    return vectorWithRandomNumbers;
}

// Common input samples
static const auto &input = randomNumbers(1024, -1.0F, 1.0F);
static const auto &inputData = input.data();
static const auto inputLength = static_cast<int>(input.size());

// Common kernel values (=impulse response, =filter coefficients)
static const auto &kernel = randomNumbers(16, 0.0F, 1.0F);
static const auto &kernelData = kernel.data();
static const auto kernelLength = static_cast<int>(kernel.size());

void directlyDerivedFromEquation(const float *const input, const int inputLength, const float *const kernel, const int kernelLength, float *const output)
{
  const auto outSize = inputLength + kernelLength - 1;
  for (auto outIndex = 0; outIndex < outSize; ++outIndex)
  {
    for (auto inputIndex = 0; inputIndex < inputLength; ++inputIndex)
    {
      const auto kernelIndex = outIndex - inputIndex;
      if ((kernelIndex >= 0) && (kernelIndex < kernelLength)) {
        output[outIndex] += (input[inputIndex] * kernel[kernelIndex]);
      }
    }
  }
}

void directlyDerivedFromEquationWithIfInOuterLoop(const float *const input, const int inputLength, const float *const kernel, const int kernelLength, float *const output)
{
  const auto outSize = inputLength + kernelLength - 1;
  for (auto outIndex = 0; outIndex < outSize; ++outIndex)
  {
    const auto outIndexPlusOne = outIndex + 1;
    const auto inputMin = (outIndexPlusOne >= kernelLength)? outIndexPlusOne - (kernelLength) : 0;
    const auto inputMax = (outIndexPlusOne < inputLength)? outIndexPlusOne: inputLength;
    for (auto inputIndex = inputMin; inputIndex < inputMax; ++inputIndex)
    {
      const auto kernelIndex = outIndex - inputIndex;
      output[outIndex] += (input[inputIndex] * kernel[kernelIndex]);
    }
  }
}

static void directlyDerivedFromEquation(benchmark::State& state) {
  // Code before the loop is not measured
  const auto outputSize = input.size() + kernel.size() - 1;
  std::vector<float> output(outputSize);
  const auto &outputData = output.data();
   
  // Code inside this loop is measured repeatedly
  for (auto _ : state) {
    directlyDerivedFromEquation(inputData, inputLength, kernelData, kernelLength, outputData);
    // Make sure the variable is not optimized away by compiler
    benchmark::DoNotOptimize(output);
  }
}
// Register the function as a benchmark
BENCHMARK(directlyDerivedFromEquation);

static void directlyDerivedFromEquationWithIfInOuterLoop(benchmark::State& state) {
  // Code before the loop is not measured
  const auto outputSize = input.size() + kernel.size() - 1;
  std::vector<float> output(outputSize);
  const auto &outputData = output.data();
    
  // Code inside this loop is measured repeatedly
  for (auto _ : state) {
    directlyDerivedFromEquationWithIfInOuterLoop(inputData, inputLength, kernelData, kernelLength, outputData);
    // Make sure the variable is not optimized away by compiler
    benchmark::DoNotOptimize(output);
  }
}
// Register the function as a benchmark
BENCHMARK(directlyDerivedFromEquationWithIfInOuterLoop);

Online Compiler

Compiler Explorer [8] is another great and widely used tool to compile code snippets online with different compilers and immediate results.

If you’ve already opened Quick C++ Benchmark, you can open Compiler Explorer by clicking “Open in Compiler Explorer”. You can also open it directly and copy the code from above into the source view. In that case you also need to add google benchmark (e.g. “trunk” version) and the code line #include <benchmark/benchmark.h> on top as shown below. Alternatively you can just delete the benchmark code and leave the implementation methods.

Use clang [9] as compiler and select for example x86-64 clang 13.0.1. Compiler options aren’t needed yet.

Compiler Explorer cano also be used to activate compiler options that give you a detailed report on what the compiler is able to optimize and what can be done to help the optimizer to get the best results.

Compiler Explorer Code

#include <vector>
#include <random>
#include <benchmark/benchmark.h>

std::vector<float> randomNumbers(int n, float min, float max)
{
    std::vector<float> vectorWithRandomNumbers(n);
    std::random_device randomDevice;
    std::mt19937 gen(randomDevice());
    std::uniform_real_distribution<float> distribution(min, max);
    for (float &value : vectorWithRandomNumbers)
    {
        value = distribution(gen);
    }
    return vectorWithRandomNumbers;
}

// Common input samples
static const auto &input = randomNumbers(1024, -1.0F, 1.0F);
static const auto &inputData = input.data();
static const auto inputLength = static_cast<int>(input.size());

// Common kernel values (=impulse response, =filter coefficients)
static const auto &kernel = randomNumbers(16, 0.0F, 1.0F);
static const auto &kernelData = kernel.data();
static const auto kernelLength = static_cast<int>(kernel.size());

void directlyDerivedFromEquation(const float *const input, const int inputLength, const float *const kernel, const int kernelLength, float *const output)
{
  const auto outSize = inputLength + kernelLength - 1;
  for (auto outIndex = 0; outIndex < outSize; ++outIndex)
  {
    for (auto inputIndex = 0; inputIndex < inputLength; ++inputIndex)
    {
      const auto kernelIndex = outIndex - inputIndex;
      if ((kernelIndex >= 0) && (kernelIndex < kernelLength)) {
        output[outIndex] += (input[inputIndex] * kernel[kernelIndex]);
      }
    }
  }
}

void directlyDerivedFromEquationWithIfInOuterLoop(const float *const input, const int inputLength, const float *const kernel, const int kernelLength, float *const output)
{
  const auto outSize = inputLength + kernelLength - 1;
  for (auto outIndex = 0; outIndex < outSize; ++outIndex)
  {
    const auto outIndexPlusOne = outIndex + 1;
    const auto inputMin = (outIndexPlusOne >= kernelLength)? outIndexPlusOne - (kernelLength) : 0;
    const auto inputMax = (outIndexPlusOne < inputLength)? outIndexPlusOne: inputLength;
    for (auto inputIndex = inputMin; inputIndex < inputMax; ++inputIndex)
    {
      const auto kernelIndex = outIndex - inputIndex;
      output[outIndex] += (input[inputIndex] * kernel[kernelIndex]);
    }
  }
}

static void directlyDerivedFromEquation(benchmark::State& state) {
  // Code before the loop is not measured
  const auto outputSize = input.size() + kernel.size() - 1;
  std::vector<float> output(outputSize);
  const auto &outputData = output.data();
   
  // Code inside this loop is measured repeatedly
  for (auto _ : state) {
    directlyDerivedFromEquation(inputData, inputLength, kernelData, kernelLength, outputData);
    // Make sure the variable is not optimized away by compiler
    benchmark::DoNotOptimize(output);
  }
}
// Register the function as a benchmark
BENCHMARK(directlyDerivedFromEquation);

static void directlyDerivedFromEquationWithIfInOuterLoop(benchmark::State& state) {
  // Code before the loop is not measured
  const auto outputSize = input.size() + kernel.size() - 1;
  std::vector<float> output(outputSize);
  const auto &outputData = output.data();
    
  // Code inside this loop is measured repeatedly
  for (auto _ : state) {
    directlyDerivedFromEquationWithIfInOuterLoop(inputData, inputLength, kernelData, kernelLength, outputData);
    // Make sure the variable is not optimized away by compiler
    benchmark::DoNotOptimize(output);
  }
}
// Register the function as a benchmark
BENCHMARK(directlyDerivedFromEquationWithIfInOuterLoop);

Compiler Options for Vectorization

Great potential for optimization is vectorization. Single Instruction Multiple Data (SIMD) makes it possible to process one operation on multiple values within one instruction. This can for example be used to multiply four values with one factor at once.

To get more insights into what the compiler is able to optimize in regard of vectorization, use the following compile options in this case specific to x86-64 clang as compiler:
-O3 -Rpass=loop-vectorize -Rpass-missed=loop-vectorize -Rpass-analysis=loop-vectorize

Compiler Explorer will show the messages from the compiler in the output view. The messages will also be shown when hovering the mouse over underlined statements like for in the code view. Both will show that the loops couldn’t be vectorized.

The message linked to the += operation of directlyDerivedFromEquationWithIfInOuterLoop is:

loop not vectorized: value that could not be identified as reduction is used outside the loop
[-Rpass-analysis=loop-vectorize]

To learn more about the compile options mentioned above, have a look at Auto-Vectorization in LLVM and Clang command line argument reference.

Unit Testing

When experimenting with the implementation it might happen that it’s behavior gets changed leading to wrong results. Unit Testing is the ideal tool to detect that. It is used to define the specification for the code and assure that it gets fulfilled in an automated way. Printing out numbers and comparing them manually might be a reasonable starting point, but should then be replaced as soon as possible.

Compiler Explorer can also be used for that. To use Catch2 [16] for Unit Testing, we need to add it as a library with at least version 3. Additionally this compile option is needed: -lCatch2Main. With the code below we can compare the results of our algorithm with precalculated reference values. Catch::Matchers::Approx is used to compare the floating point values that might differ slightly due to rounding errors. If there is a significant difference, the test will fail.

Unit Tests

Add Catch2 Library v3 and Compile Option -lCatch2Main in Compiler Explorer.

#include <vector>
#include "catch2/catch_test_macros.hpp"
#include "catch2/matchers/catch_matchers_vector.hpp"

const std::vector<float> randomSize32 = {
    3.412001133e-01F,
    -7.189993262e-01F,
    1.750426292e-01F,
    -9.811252952e-01F,
    2.045263052e-01F,
    4.684762955e-01F,
    6.160235405e-02F,
    5.106519461e-01F,
    -1.739602089e-01F,
    -6.787777543e-01F,
    -2.564323545e-01F,
    3.146402836e-01F,
    3.727546930e-01F,
    7.325013876e-01F,
    6.668845415e-01F,
    -7.007303238e-01F,
    -1.356991529e-01F,
    -3.637151718e-01F,
    2.377008200e-01F,
    5.763622522e-01F,
    7.675963640e-01F,
    5.417956114e-01F,
    5.251662731e-01F,
    2.914607525e-01F,
    -2.455517054e-01F,
    1.925699711e-01F,
    2.517737150e-01F,
    2.002975941e-01F,
    -6.586538553e-01F,
    7.387914658e-01F,
    -3.581553698e-02F,
    9.342098236e-01F,
};

const std::vector<float> waveletFilterCoefficientsDaubechies16 = {
    5.44158422430000010E-02,
    3.12871590914000020E-01F,
    6.75630736296999990E-01F,
    5.85354683654000010E-01F,
    -1.58291052559999990E-02F,
    -2.84015542961999990E-01F,
    4.72484573999999990E-04F,
    1.28747426619999990E-01F,
    -1.73693010020000010E-02F,
    -4.40882539310000000E-02F,
    1.39810279170000000E-02F,
    8.74609404700000050E-03F,
    -4.87035299299999960E-03F,
    -3.91740372999999990E-04F,
    6.75449405999999950E-04F,
    -1.17476784000000000E-04F
};

const std::vector<float> convolutionReferenceResultOfRandomSize32WithDaubechies16 = {
    1.856669039e-02F,
    6.762687862e-02F,
    1.509590354e-02F,
    -2.846778631e-01F,
    -6.038430929e-01F,
    -5.564584136e-01F,
    -8.459951729e-02F,
    4.927030504e-01F,
    6.431518793e-01F,
    2.437220365e-01F,
    -2.717656195e-01F,
    -6.203101873e-01F,
    -4.995880723e-01F,
    2.613126636e-01F,
    9.362079501e-01F,
    9.296823144e-01F,
    4.550002515e-01F,
    -2.715559006e-01F,
    -7.444483638e-01F,
    -3.568022251e-01F,
    4.363469481e-01F,
    9.047260284e-01F,
    1.028757334e+00F,
    8.956634998e-01F,
    5.741767287e-01F,
    2.471363544e-01F,
    -8.406746201e-03F,
    -1.803561347e-03F,
    2.634630501e-01F,
    2.194332480e-01F,
    -1.380935758e-01F,
    2.997516282e-02F,
    6.787298918e-01F,
    8.316706419e-01F,
    3.469930291e-01F,
    -1.044505164e-01F,
    -1.610428244e-01F,
    1.633273438e-02F,
    7.936858386e-02F,
    -1.099434309e-02F,
    -3.195003048e-02F,
    9.513526224e-03F,
    7.587288972e-03F,
    -3.959508147e-03F,
    -4.769501393e-04F,
    6.352189230e-04F,
    -1.097479617e-04F
};

const auto &input = randomSize32;
const auto &inputData = input.data();
const auto inputLength = static_cast<int>(input.size());

// Common kernel values (=impulse response, =filter coefficients)
const auto &kernel = waveletFilterCoefficientsDaubechies16;
const auto &kernelData = kernel.data();
const auto kernelLength = static_cast<int>(kernel.size());

// Precalculated result of the convolution as a reference
const auto &reference = convolutionReferenceResultOfRandomSize32WithDaubechies16;

void directlyDerivedFromEquation(const float *const input, const int inputLength, const float *const kernel, const int kernelLength, float *const output)
{
  const auto outSize = inputLength + kernelLength - 1;
  for (auto outIndex = 0; outIndex < outSize; ++outIndex)
  {
    for (auto inputIndex = 0; inputIndex < inputLength; ++inputIndex)
    {
      const auto kernelIndex = outIndex - inputIndex;
      if ((kernelIndex >= 0) && (kernelIndex < kernelLength)) {
        output[outIndex] += (input[inputIndex] * kernel[kernelIndex]);
      }
    }
  }
}

void directlyDerivedFromEquationWithIfInOuterLoop(const float *const input, const int inputLength, const float *const kernel, const int kernelLength, float *const output)
{
  const auto outSize = inputLength + kernelLength - 1;
  for (auto outIndex = 0; outIndex < outSize; ++outIndex)
  {
    const auto outIndexPlusOne = outIndex + 1;
    const auto inputMin = (outIndexPlusOne >= kernelLength)? outIndexPlusOne - (kernelLength) : 0;
    const auto inputMax = (outIndexPlusOne < inputLength)? outIndexPlusOne: inputLength;
    for (auto inputIndex = inputMin; inputIndex < inputMax; ++inputIndex)
    {
      const auto kernelIndex = outIndex - inputIndex;
      output[outIndex] += (input[inputIndex] * kernel[kernelIndex]);
    }
  }
}

TEST_CASE("directlyDerivedFromEquation is correct", "[convolution]") {
    const auto outputSize = input.size() + kernel.size() - 1;
    std::vector<float> output(outputSize);
    const auto &outputData = output.data();

    directlyDerivedFromEquation(inputData, inputLength, kernelData, kernelLength, outputData);
    REQUIRE_THAT(output, Catch::Matchers::Approx(reference));
}

TEST_CASE("directlyDerivedFromEquationWithIfInOuterLoop is correct", "[convolution]") {
    const auto outputSize = input.size() + kernel.size() - 1;
    std::vector<float> output(outputSize);
    const auto &outputData = output.data();

    directlyDerivedFromEquationWithIfInOuterLoop(inputData, inputLength, kernelData, kernelLength, outputData);
    REQUIRE_THAT(output, Catch::Matchers::Approx(reference));
}

Optimization for Speed and Maintainability

Prepared with tools to measure and analyze the code easily, we now can continue to optimize it.

Without the restriction to stay maintainable, we’ll sooner or later get in touch with the Intel® Intrinsics Guide [10] and start writing CPU instruction set dependent code or use an abstraction that leads to additional dependencies with all the complexity that comes with that. As we’ll see later, stunning speed can be achieved with this approach.

However, with maintainability in mind, we’ll have a look at how far we can get with the build-in optimization capabilities of the compiler(s). That requires the algorithm and it’s implementation to be layed out in a way that the compiler can get most out of it.

Reevaluate the Algorithm

Let’s go back to the equation and see, if the algorithm can be written in a different way:

\[(x * h)[n] = \sum_{i=0}^{M} x[n-i]h[i]\]

Since finite impulse response (FIR) filters are essentially Convolution implementations, we can borrow ideas from articles like Pipelined Direct Form FIR Versus the Transposed Structure [11]. The described Transposed Structure has a very interesting property: The order of the filter coefficients \(h[i]\) is reversed. This has great potential because the array indices would always be positive. Would it then be possible to get rid of all if statements (branches)?

Experiment with Simple Input Signals

Let’s experiment with different input signals to get familiar with the behavior of the Convolution.

1. What happens if the input signal is 1 for index = 0 and 0 in all other cases?

   \[x(n)= \begin{cases} 1, & \text{for } n = 0\\ 0, & \text{otherwise} \end{cases}\]

   This input signal is related to the Dirac delta [17]. It is adapted for discrete signals and called discrete unit sample function [18]. The output in response to this input signal is known as impulse response.

   The result of the sum in the equation above will be zero for all values except for index \(i = n\), because \(x[i - n]\) becomes \(x[0]\) which is 1. In that case the result is \(h[i = n]\). So we can simply write:

   \[=> (x * h)[n] = h[n]\]
   • For the implementation this means that the values of array \(h[n]\) are copied to the output array as they are.

2. What happens if the input signal is scaled by 2 for index = 0 and 0 in all other cases?

   \[x(n)= \begin{cases} s=2, & \text{for } n = 0\\ 0, & \text{otherwise} \end{cases}\]

   The behavior is the same as above except that the response is scaled because the values of \(h[n]\) are multiplied with \(s=2=x[0]\). This leads us to:

   \[=> (x * h)[n] = s \cdot h[n]\]
   • For the implementation this means that every value of array \(h[i]\) is multiplied by \(x[0] = s\) and then copied to the output array.

3. What happens if the input signal is delayed by 1 sample so it is 2 for index = 1 and 0 in all other cases?

   \[x(n)= \begin{cases} s=2, & \text{for } n = d=1\\ 0, & \text{otherwise} \end{cases}\]

   The behavior is similar except for the time shift, that corresponds to the time shift of the input signal. This leads us to:

   \[=> (x * h)[n] = s \cdot h[n - d]\]
   • For the implementation this means that the values of array \(h[n]\) are placed at the same index as their corresponding value of the input signal.

4. Finally, what happens if our input signal is 1 for index = 0, 2 for the index = 1 and 0 in all other cases?

   This is where the sum comes into play. We take both elements from above and simply add both output arrays element by element:

   \[x(n)= \begin{cases} 1, & \text{for } n = 0\\ s, & \text{for } n = d \not = 0\\ 0, & \text{otherwise} \end{cases}\] \[=> (x * h)[n] = 1 \cdot h[n] + s \cdot h[n - d]\]

Implementing the Transposed Structure

From the experiments above we can derive new requirements for the implementation:

• The array \(h[n]\) (=kernel =impulse response =filter coefficients) needs to be copied to the output array.
• This needs to be done for every input signal value.
• The input value is used to scale \(h[n]\), which means that every value of \(h[n]\) is multiplied with that value.
• The index (location in time) of the input signal determines at which index of the output array the scaled \(h[n]\) values are placed (shift).
• Whenever an output value is written, it is added to the previous value that existed there (sum).

In terms of code we can therefore write:

void kernelPerInputValueTransposed(
  const float *const input, 
  const int inputLength, 
  const float *const kernel, 
  const int kernelLength, 
  float *const output)
{
  for (auto inputIndex = 0; inputIndex < inputLength; ++inputIndex)
  {
    for (auto kernelIndex = 0; kernelIndex < kernelLength; ++kernelIndex)
    {
      output[inputIndex + kernelIndex] += kernel[kernelIndex] * input[inputIndex];
    }
  }
}

By implementing Convolution with the Transposed Structure, there is no need for if statements (branches) inside the loops any more. Although loops also imply branches with their loop condition, modern compilers are able to optimize them under certain circumstances. So let’s measure and analyze the new implementation.

Performance of the Transposed Structure

Using Quick C++ Benchmark [7] to compare the optimized direct with the transposed structure implementation shows us the following result. The Transposed Structure is nearly twice as fast as the previously optimized implementation.

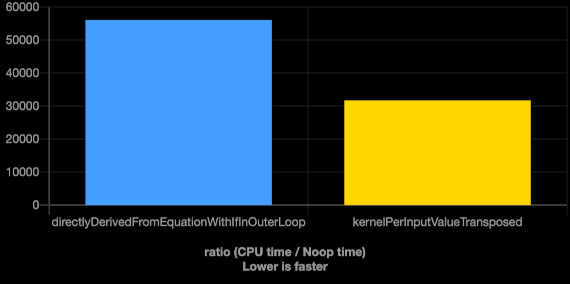
Benchmark Code

#include <vector>
#include <random>

std::vector<float> randomNumbers(int n, float min, float max)
{
    std::vector<float> vectorWithRandomNumbers(n);
    std::random_device randomDevice;
    std::mt19937 gen(randomDevice());
    std::uniform_real_distribution<float> distribution(min, max);
    for (float &value : vectorWithRandomNumbers)
    {
        value = distribution(gen);
    }
    return vectorWithRandomNumbers;
}

// Common input samples
static const auto &input = randomNumbers(1024, -1.0F, 1.0F);
static const auto &inputData = input.data();
static const auto inputLength = static_cast<int>(input.size());

// Common kernel values (=impulse response, =filter coefficients)
static const auto &kernel = randomNumbers(16, 0.0F, 1.0F);
static const auto &kernelData = kernel.data();
static const auto kernelLength = static_cast<int>(kernel.size());

void directlyDerivedFromEquationWithIfInOuterLoop(const float *const input, const int inputLength, const float *const kernel, const int kernelLength, float *const output)
{
  const auto outSize = inputLength + kernelLength - 1;
  for (auto outIndex = 0; outIndex < outSize; ++outIndex)
  {
    const auto outIndexPlusOne = outIndex + 1;
    const auto inputMin = (outIndexPlusOne >= kernelLength)? outIndexPlusOne - (kernelLength) : 0;
    const auto inputMax = (outIndexPlusOne < inputLength)? outIndexPlusOne: inputLength;
    for (auto inputIndex = inputMin; inputIndex < inputMax; ++inputIndex)
    {
      const auto kernelIndex = outIndex - inputIndex;
      output[outIndex] += (input[inputIndex] * kernel[kernelIndex]);
    }
  }
}

void kernelPerInputValueTransposed(const float *const input, const int inputLength, const float *const kernel, const int kernelLength, float *const output)
{
  for (auto inputIndex = 0; inputIndex < inputLength; ++inputIndex)
  {
    for (auto kernelIndex = 0; kernelIndex < kernelLength; ++kernelIndex)
    {
      output[inputIndex + kernelIndex] += kernel[kernelIndex] * input[inputIndex];
    }
  }
}

static void directlyDerivedFromEquationWithIfInOuterLoop(benchmark::State& state) {
  // Code before the loop is not measured
  const auto outputSize = input.size() + kernel.size() - 1;
  std::vector<float> output(outputSize);
  const auto &outputData = output.data();
    
  // Code inside this loop is measured repeatedly
  for (auto _ : state) {
    directlyDerivedFromEquationWithIfInOuterLoop(inputData, inputLength, kernelData, kernelLength, outputData);
    // Make sure the variable is not optimized away by compiler
    benchmark::DoNotOptimize(output);
  }
}
// Register the function as a benchmark
BENCHMARK(directlyDerivedFromEquationWithIfInOuterLoop);

static void kernelPerInputValueTransposed(benchmark::State& state) {
  // Code before the loop is not measured
  const auto outputSize = input.size() + kernel.size() - 1;
  std::vector<float> output(outputSize);
  const auto &outputData = output.data();
    
  // Code inside this loop is measured repeatedly
  for (auto _ : state) {
    kernelPerInputValueTransposed(inputData, inputLength, kernelData, kernelLength, outputData);
    // Make sure the variable is not optimized away by compiler
    benchmark::DoNotOptimize(output);
  }
}
// Register the function as a benchmark
BENCHMARK(kernelPerInputValueTransposed);

Unit Tests

Add Catch2 Library v3 and Compile Option -lCatch2Main in Compiler Explorer.

#include <vector>
#include "catch2/catch_test_macros.hpp"
#include "catch2/matchers/catch_matchers_vector.hpp"

const std::vector<float> randomSize32 = {
    3.412001133e-01F,
    -7.189993262e-01F,
    1.750426292e-01F,
    -9.811252952e-01F,
    2.045263052e-01F,
    4.684762955e-01F,
    6.160235405e-02F,
    5.106519461e-01F,
    -1.739602089e-01F,
    -6.787777543e-01F,
    -2.564323545e-01F,
    3.146402836e-01F,
    3.727546930e-01F,
    7.325013876e-01F,
    6.668845415e-01F,
    -7.007303238e-01F,
    -1.356991529e-01F,
    -3.637151718e-01F,
    2.377008200e-01F,
    5.763622522e-01F,
    7.675963640e-01F,
    5.417956114e-01F,
    5.251662731e-01F,
    2.914607525e-01F,
    -2.455517054e-01F,
    1.925699711e-01F,
    2.517737150e-01F,
    2.002975941e-01F,
    -6.586538553e-01F,
    7.387914658e-01F,
    -3.581553698e-02F,
    9.342098236e-01F,
};

const std::vector<float> waveletFilterCoefficientsDaubechies16 = {
    5.44158422430000010E-02,
    3.12871590914000020E-01F,
    6.75630736296999990E-01F,
    5.85354683654000010E-01F,
    -1.58291052559999990E-02F,
    -2.84015542961999990E-01F,
    4.72484573999999990E-04F,
    1.28747426619999990E-01F,
    -1.73693010020000010E-02F,
    -4.40882539310000000E-02F,
    1.39810279170000000E-02F,
    8.74609404700000050E-03F,
    -4.87035299299999960E-03F,
    -3.91740372999999990E-04F,
    6.75449405999999950E-04F,
    -1.17476784000000000E-04F
};

const std::vector<float> convolutionReferenceResultOfRandomSize32WithDaubechies16 = {
    1.856669039e-02F,
    6.762687862e-02F,
    1.509590354e-02F,
    -2.846778631e-01F,
    -6.038430929e-01F,
    -5.564584136e-01F,
    -8.459951729e-02F,
    4.927030504e-01F,
    6.431518793e-01F,
    2.437220365e-01F,
    -2.717656195e-01F,
    -6.203101873e-01F,
    -4.995880723e-01F,
    2.613126636e-01F,
    9.362079501e-01F,
    9.296823144e-01F,
    4.550002515e-01F,
    -2.715559006e-01F,
    -7.444483638e-01F,
    -3.568022251e-01F,
    4.363469481e-01F,
    9.047260284e-01F,
    1.028757334e+00F,
    8.956634998e-01F,
    5.741767287e-01F,
    2.471363544e-01F,
    -8.406746201e-03F,
    -1.803561347e-03F,
    2.634630501e-01F,
    2.194332480e-01F,
    -1.380935758e-01F,
    2.997516282e-02F,
    6.787298918e-01F,
    8.316706419e-01F,
    3.469930291e-01F,
    -1.044505164e-01F,
    -1.610428244e-01F,
    1.633273438e-02F,
    7.936858386e-02F,
    -1.099434309e-02F,
    -3.195003048e-02F,
    9.513526224e-03F,
    7.587288972e-03F,
    -3.959508147e-03F,
    -4.769501393e-04F,
    6.352189230e-04F,
    -1.097479617e-04F
};

const auto &input = randomSize32;
const auto &inputData = input.data();
const auto inputLength = static_cast<int>(input.size());

// Common kernel values (=impulse response, =filter coefficients)
const auto &kernel = waveletFilterCoefficientsDaubechies16;
const auto &kernelData = kernel.data();
const auto kernelLength = static_cast<int>(kernel.size());

// Precalculated result of the convolution as a reference
const auto &reference = convolutionReferenceResultOfRandomSize32WithDaubechies16;

void directlyDerivedFromEquation(const float *const input, const int inputLength, const float *const kernel, const int kernelLength, float *const output)
{
  const auto outSize = inputLength + kernelLength - 1;
  for (auto outIndex = 0; outIndex < outSize; ++outIndex)
  {
    for (auto inputIndex = 0; inputIndex < inputLength; ++inputIndex)
    {
      const auto kernelIndex = outIndex - inputIndex;
      if ((kernelIndex >= 0) && (kernelIndex < kernelLength)) {
        output[outIndex] += (input[inputIndex] * kernel[kernelIndex]);
      }
    }
  }
}

void directlyDerivedFromEquationWithIfInOuterLoop(const float *const input, const int inputLength, const float *const kernel, const int kernelLength, float *const output)
{
  const auto outSize = inputLength + kernelLength - 1;
  for (auto outIndex = 0; outIndex < outSize; ++outIndex)
  {
    const auto outIndexPlusOne = outIndex + 1;
    const auto inputMin = (outIndexPlusOne >= kernelLength)? outIndexPlusOne - (kernelLength) : 0;
    const auto inputMax = (outIndexPlusOne < inputLength)? outIndexPlusOne: inputLength;
    for (auto inputIndex = inputMin; inputIndex < inputMax; ++inputIndex)
    {
      const auto kernelIndex = outIndex - inputIndex;
      output[outIndex] += (input[inputIndex] * kernel[kernelIndex]);
    }
  }
}

void kernelPerInputValueTransposed(const float *const input, const int inputLength, const float *const kernel, const int kernelLength, float *const output)
{
  for (auto inputIndex = 0; inputIndex < inputLength; ++inputIndex)
  {
    for (auto kernelIndex = 0; kernelIndex < kernelLength; ++kernelIndex)
    {
      output[inputIndex + kernelIndex] += kernel[kernelIndex] * input[inputIndex];
    }
  }
}

TEST_CASE("directlyDerivedFromEquation is correct", "[convolution]") {
    const auto outputSize = input.size() + kernel.size() - 1;
    std::vector<float> output(outputSize);
    const auto &outputData = output.data();

    directlyDerivedFromEquation(inputData, inputLength, kernelData, kernelLength, outputData);
    REQUIRE_THAT(output, Catch::Matchers::Approx(reference));
}

TEST_CASE("directlyDerivedFromEquationWithIfInOuterLoop is correct", "[convolution]") {
    const auto outputSize = input.size() + kernel.size() - 1;
    std::vector<float> output(outputSize);
    const auto &outputData = output.data();

    directlyDerivedFromEquationWithIfInOuterLoop(inputData, inputLength, kernelData, kernelLength, outputData);
    REQUIRE_THAT(output, Catch::Matchers::Approx(reference));
}

TEST_CASE("kernelPerInputValueTransposed is correct", "[convolution]") {
    const auto outputSize = input.size() + kernel.size() - 1;
    std::vector<float> output(outputSize);
    const auto &outputData = output.data();

    kernelPerInputValueTransposed(inputData, inputLength, kernelData, kernelLength, outputData);
    REQUIRE_THAT(output, Catch::Matchers::Approx(reference));
}

Compiler Output of the Transposed Structure

As described above in Compiler Option for Vectorization we can use Compiler Explorer with the same compiler options to see, if the Clang compiler was able to apply auto vectorization. The output message looks promising:

vectorized loop (vectorization width: 4, interleaved count: 2) [-Rpass=loop-vectorize]

Optimize for Microsoft Visual Studio (MSVC)

When switching to “x64 msvc v19.latest” in Compiler Explorer we first need to delete the benchmark code lines. They aren’t needed here anyway, since we are interested in the compiler output for the Convolution implementations.

The compiler options need to be changed to /O2 /Qvec-report:2 for MSVC as described in Auto-Vectorizer Reporting Level [13] and Auto-Parallelization and Auto-Vectorization [14].

The result is not as we might hoped:

info C5002: loop not vectorized due to reason '1203'

To anticipate the results of troubleshooting and research, the following implementation works fine with Clang, MSVC and GCC:

void kernelPerInputValueTransposed(
  const float *const input, 
  const int inputLength, 
  const float *const kernel, 
  const int kernelLength, 
  float *const output)
{
  for (auto inputIndex = 0; inputIndex < inputLength; ++inputIndex)
  {
    // Makes it obvious for the compiler (especially MSVC) that the factor is constant.
    // Otherwise this message occurs: "1203: Loop body includes on-contiguous accesses into an array".
    const auto inputValue = input[inputIndex];

    for (auto kernelIndex = 0; kernelIndex < kernelLength; ++kernelIndex)
    {
      // It seems to be beneficial to put the constant factor last when MSVC compile option "/fp:fast" is activated.
      output[inputIndex + kernelIndex] += kernel[kernelIndex] * inputValue;
    }
  }
}

Unit Tests

Add Catch2 Library v3 and Compile Option -lCatch2Main in Compiler Explorer.

#include <vector>
#include "catch2/catch_test_macros.hpp"
#include "catch2/matchers/catch_matchers_vector.hpp"

const std::vector<float> randomSize32 = {
    3.412001133e-01F,
    -7.189993262e-01F,
    1.750426292e-01F,
    -9.811252952e-01F,
    2.045263052e-01F,
    4.684762955e-01F,
    6.160235405e-02F,
    5.106519461e-01F,
    -1.739602089e-01F,
    -6.787777543e-01F,
    -2.564323545e-01F,
    3.146402836e-01F,
    3.727546930e-01F,
    7.325013876e-01F,
    6.668845415e-01F,
    -7.007303238e-01F,
    -1.356991529e-01F,
    -3.637151718e-01F,
    2.377008200e-01F,
    5.763622522e-01F,
    7.675963640e-01F,
    5.417956114e-01F,
    5.251662731e-01F,
    2.914607525e-01F,
    -2.455517054e-01F,
    1.925699711e-01F,
    2.517737150e-01F,
    2.002975941e-01F,
    -6.586538553e-01F,
    7.387914658e-01F,
    -3.581553698e-02F,
    9.342098236e-01F,
};

// Common input samples
const std::vector<float> waveletFilterCoefficientsDaubechies16 = {
    5.44158422430000010E-02,
    3.12871590914000020E-01F,
    6.75630736296999990E-01F,
    5.85354683654000010E-01F,
    -1.58291052559999990E-02F,
    -2.84015542961999990E-01F,
    4.72484573999999990E-04F,
    1.28747426619999990E-01F,
    -1.73693010020000010E-02F,
    -4.40882539310000000E-02F,
    1.39810279170000000E-02F,
    8.74609404700000050E-03F,
    -4.87035299299999960E-03F,
    -3.91740372999999990E-04F,
    6.75449405999999950E-04F,
    -1.17476784000000000E-04F
};

const std::vector<float> convolutionReferenceResultOfRandomSize32WithDaubechies16 = {
    1.856669039e-02F,
    6.762687862e-02F,
    1.509590354e-02F,
    -2.846778631e-01F,
    -6.038430929e-01F,
    -5.564584136e-01F,
    -8.459951729e-02F,
    4.927030504e-01F,
    6.431518793e-01F,
    2.437220365e-01F,
    -2.717656195e-01F,
    -6.203101873e-01F,
    -4.995880723e-01F,
    2.613126636e-01F,
    9.362079501e-01F,
    9.296823144e-01F,
    4.550002515e-01F,
    -2.715559006e-01F,
    -7.444483638e-01F,
    -3.568022251e-01F,
    4.363469481e-01F,
    9.047260284e-01F,
    1.028757334e+00F,
    8.956634998e-01F,
    5.741767287e-01F,
    2.471363544e-01F,
    -8.406746201e-03F,
    -1.803561347e-03F,
    2.634630501e-01F,
    2.194332480e-01F,
    -1.380935758e-01F,
    2.997516282e-02F,
    6.787298918e-01F,
    8.316706419e-01F,
    3.469930291e-01F,
    -1.044505164e-01F,
    -1.610428244e-01F,
    1.633273438e-02F,
    7.936858386e-02F,
    -1.099434309e-02F,
    -3.195003048e-02F,
    9.513526224e-03F,
    7.587288972e-03F,
    -3.959508147e-03F,
    -4.769501393e-04F,
    6.352189230e-04F,
    -1.097479617e-04F
};

const auto &input = randomSize32;
const auto &inputData = input.data();
const auto inputLength = static_cast<int>(input.size());

// Common kernel values (=impulse response, =filter coefficients)
const auto &kernel = waveletFilterCoefficientsDaubechies16;
const auto &kernelData = kernel.data();
const auto kernelLength = static_cast<int>(kernel.size());

// Precalculated result of the convolution as a reference
const auto &reference = convolutionReferenceResultOfRandomSize32WithDaubechies16;

void directlyDerivedFromEquation(const float *const input, const int inputLength, const float *const kernel, const int kernelLength, float *const output)
{
  const auto outSize = inputLength + kernelLength - 1;
  for (auto outIndex = 0; outIndex < outSize; ++outIndex)
  {
    for (auto inputIndex = 0; inputIndex < inputLength; ++inputIndex)
    {
      const auto kernelIndex = outIndex - inputIndex;
      if ((kernelIndex >= 0) && (kernelIndex < kernelLength)) {
        output[outIndex] += (input[inputIndex] * kernel[kernelIndex]);
      }
    }
  }
}

void directlyDerivedFromEquationWithIfInOuterLoop(const float *const input, const int inputLength, const float *const kernel, const int kernelLength, float *const output)
{
  const auto outSize = inputLength + kernelLength - 1;
  for (auto outIndex = 0; outIndex < outSize; ++outIndex)
  {
    const auto outIndexPlusOne = outIndex + 1;
    const auto inputMin = (outIndexPlusOne >= kernelLength)? outIndexPlusOne - (kernelLength) : 0;
    const auto inputMax = (outIndexPlusOne < inputLength)? outIndexPlusOne: inputLength;
    for (auto inputIndex = inputMin; inputIndex < inputMax; ++inputIndex)
    {
      const auto kernelIndex = outIndex - inputIndex;
      output[outIndex] += (input[inputIndex] * kernel[kernelIndex]);
    }
  }
}

void kernelPerInputValueTransposed(const float *const input, const int inputLength, const float *const kernel, const int kernelLength, float *const output)
{
    for (auto inputIndex = 0; inputIndex < inputLength; ++inputIndex)
    {
        // Makes it obvious for the compiler (especially MSVC) that the factor is constant.
        // Otherwise this message occurs: "1203: Loop body includes on-contiguous accesses into an array".
        const auto inputValue = input[inputIndex];

        for (auto kernelIndex = 0; kernelIndex < kernelLength; ++kernelIndex)
        {
            // It seems to be beneficial to put the constant factor last when MSVC compile option "/fp:fast" is activated.
            output[inputIndex + kernelIndex] += kernel[kernelIndex] * inputValue;
        }
    }
}

TEST_CASE("directlyDerivedFromEquation is correct", "[convolution]") {
    const auto outputSize = input.size() + kernel.size() - 1;
    std::vector<float> output(outputSize);
    const auto &outputData = output.data();

    directlyDerivedFromEquation(inputData, inputLength, kernelData, kernelLength, outputData);
    REQUIRE_THAT(output, Catch::Matchers::Approx(reference));
}

TEST_CASE("directlyDerivedFromEquationWithIfInOuterLoop is correct", "[convolution]") {
    const auto outputSize = input.size() + kernel.size() - 1;
    std::vector<float> output(outputSize);
    const auto &outputData = output.data();

    directlyDerivedFromEquationWithIfInOuterLoop(inputData, inputLength, kernelData, kernelLength, outputData);
    REQUIRE_THAT(output, Catch::Matchers::Approx(reference));
}

TEST_CASE("kernelPerInputValueTransposed is correct", "[convolution]") {
    const auto outputSize = input.size() + kernel.size() - 1;
    std::vector<float> output(outputSize);
    const auto &outputData = output.data();

    kernelPerInputValueTransposed(inputData, inputLength, kernelData, kernelLength, outputData);
    REQUIRE_THAT(output, Catch::Matchers::Approx(reference));
}

Cache Efficiency

As mentioned at the beginning, it is assumed that the kernel length lies between 10 and 200. Convolution for much larger kernels will most certainly benefit from the Fast Fourier Transformation (FFT). For much smaller kernels there are other options like Winograd’s minimal filtering algorithm that might be considered.

This leads to the assumption, that the input length is significantly larger than the kernel length. The question arises whether it would make sense to swap the loops. The idea behind that is that a lot of operations with a constant value should be faster because it will only be loaded once from memory and is then cached. Let’s measure both variants.

Measure Loop Order

As the result shows, iterating over the larger array in the inner loop makes the implementation about 3 to 4 times faster. This might not only be a cause of efficient caching. Auto vectorization focuses on the inner loop, so it is beneficial if the optimized loop is the larger one.

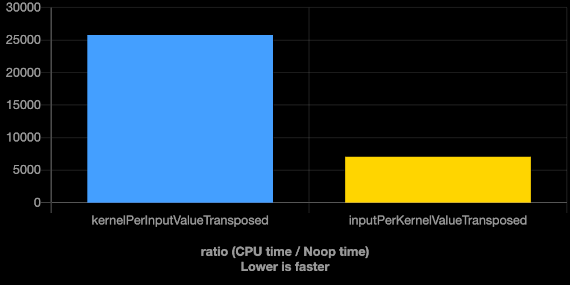
Benchmark Code

#include <vector>
#include <random>

std::vector<float> randomNumbers(int n, float min, float max)
{
    std::vector<float> vectorWithRandomNumbers(n);
    std::random_device randomDevice;
    std::mt19937 gen(randomDevice());
    std::uniform_real_distribution<float> distribution(min, max);
    for (float &value : vectorWithRandomNumbers)
    {
        value = distribution(gen);
    }
    return vectorWithRandomNumbers;
}

// Common input samples
static const auto &input = randomNumbers(1024, -1.0F, 1.0F);
static const auto &inputData = input.data();
static const auto inputLength = static_cast<int>(input.size());

// Common kernel values (=impulse response, =filter coefficients)
static const auto &kernel = randomNumbers(16, 0.0F, 1.0F);
static const auto &kernelData = kernel.data();
static const auto kernelLength = static_cast<int>(kernel.size());

void kernelPerInputValueTransposed(const float *const input, const int inputLength, const float *const kernel, const int kernelLength, float *const output)
{
    for (auto inputIndex = 0; inputIndex < inputLength; ++inputIndex)
    {
        // Makes it obvious for the compiler (especially MSVC) that the factor is constant.
        // Otherwise this message occurs: "1203: Loop body includes on-contiguous accesses into an array".
        const auto inputValue = input[inputIndex];

        for (auto kernelIndex = 0; kernelIndex < kernelLength; ++kernelIndex)
        {
            // It seems to be beneficial to put the constant factor last when MSVC compile option "/fp:fast" is activated.
            output[inputIndex + kernelIndex] += kernel[kernelIndex] * inputValue;
        }
    }
}

void inputPerKernelValueTransposed(const float *const input, const int inputLength, const float *const kernel, const int kernelLength, float *const output)
{
    for (auto kernelIndex = 0; kernelIndex < kernelLength; ++kernelIndex)
    {
        // Makes it obvious for the compiler (especially MSVC) that the factor is constant.
        // Otherwise this message occurs: "1203: Loop body includes on-contiguous accesses into an array".
        const auto kernelValue = kernel[kernelIndex];

        for (auto inputIndex = 0; inputIndex < inputLength; ++inputIndex)
        {
            // It seems to be beneficial to put the constant factor last when MSVC compile option "/fp:fast" is activated.
            output[inputIndex + kernelIndex] += input[inputIndex] * kernelValue;
        }
    }
}

static void kernelPerInputValueTransposed(benchmark::State& state) {
  // Code before the loop is not measured
  const auto outputSize = input.size() + kernel.size() - 1;
  std::vector<float> output(outputSize);
  const auto &outputData = output.data();
    
  // Code inside this loop is measured repeatedly
  for (auto _ : state) {
    kernelPerInputValueTransposed(inputData, inputLength, kernelData, kernelLength, outputData);
    // Make sure the variable is not optimized away by compiler
    benchmark::DoNotOptimize(output);
  }
}
// Register the function as a benchmark
BENCHMARK(kernelPerInputValueTransposed);

static void inputPerKernelValueTransposed(benchmark::State& state) {
  // Code before the loop is not measured
  const auto outputSize = input.size() + kernel.size() - 1;
  std::vector<float> output(outputSize);
  const auto &outputData = output.data();
    
  // Code inside this loop is measured repeatedly
  for (auto _ : state) {
    inputPerKernelValueTransposed(inputData, inputLength, kernelData, kernelLength, outputData);
    // Make sure the variable is not optimized away by compiler
    benchmark::DoNotOptimize(output);
  }
}
// Register the function as a benchmark
BENCHMARK(inputPerKernelValueTransposed);

Unit Tests

Add Catch2 Library v3 and Compile Option -lCatch2Main in Compiler Explorer.

#include <vector>
#include "catch2/catch_test_macros.hpp"
#include "catch2/matchers/catch_matchers_vector.hpp"

const std::vector<float> randomSize32 = {
    3.412001133e-01F,
    -7.189993262e-01F,
    1.750426292e-01F,
    -9.811252952e-01F,
    2.045263052e-01F,
    4.684762955e-01F,
    6.160235405e-02F,
    5.106519461e-01F,
    -1.739602089e-01F,
    -6.787777543e-01F,
    -2.564323545e-01F,
    3.146402836e-01F,
    3.727546930e-01F,
    7.325013876e-01F,
    6.668845415e-01F,
    -7.007303238e-01F,
    -1.356991529e-01F,
    -3.637151718e-01F,
    2.377008200e-01F,
    5.763622522e-01F,
    7.675963640e-01F,
    5.417956114e-01F,
    5.251662731e-01F,
    2.914607525e-01F,
    -2.455517054e-01F,
    1.925699711e-01F,
    2.517737150e-01F,
    2.002975941e-01F,
    -6.586538553e-01F,
    7.387914658e-01F,
    -3.581553698e-02F,
    9.342098236e-01F,
};

// Common input samples
const std::vector<float> waveletFilterCoefficientsDaubechies16 = {
    5.44158422430000010E-02,
    3.12871590914000020E-01F,
    6.75630736296999990E-01F,
    5.85354683654000010E-01F,
    -1.58291052559999990E-02F,
    -2.84015542961999990E-01F,
    4.72484573999999990E-04F,
    1.28747426619999990E-01F,
    -1.73693010020000010E-02F,
    -4.40882539310000000E-02F,
    1.39810279170000000E-02F,
    8.74609404700000050E-03F,
    -4.87035299299999960E-03F,
    -3.91740372999999990E-04F,
    6.75449405999999950E-04F,
    -1.17476784000000000E-04F
};

const std::vector<float> convolutionReferenceResultOfRandomSize32WithDaubechies16 = {
    1.856669039e-02F,
    6.762687862e-02F,
    1.509590354e-02F,
    -2.846778631e-01F,
    -6.038430929e-01F,
    -5.564584136e-01F,
    -8.459951729e-02F,
    4.927030504e-01F,
    6.431518793e-01F,
    2.437220365e-01F,
    -2.717656195e-01F,
    -6.203101873e-01F,
    -4.995880723e-01F,
    2.613126636e-01F,
    9.362079501e-01F,
    9.296823144e-01F,
    4.550002515e-01F,
    -2.715559006e-01F,
    -7.444483638e-01F,
    -3.568022251e-01F,
    4.363469481e-01F,
    9.047260284e-01F,
    1.028757334e+00F,
    8.956634998e-01F,
    5.741767287e-01F,
    2.471363544e-01F,
    -8.406746201e-03F,
    -1.803561347e-03F,
    2.634630501e-01F,
    2.194332480e-01F,
    -1.380935758e-01F,
    2.997516282e-02F,
    6.787298918e-01F,
    8.316706419e-01F,
    3.469930291e-01F,
    -1.044505164e-01F,
    -1.610428244e-01F,
    1.633273438e-02F,
    7.936858386e-02F,
    -1.099434309e-02F,
    -3.195003048e-02F,
    9.513526224e-03F,
    7.587288972e-03F,
    -3.959508147e-03F,
    -4.769501393e-04F,
    6.352189230e-04F,
    -1.097479617e-04F
};

const auto &input = randomSize32;
const auto &inputData = input.data();
const auto inputLength = static_cast<int>(input.size());

// Common kernel values (=impulse response, =filter coefficients)
const auto &kernel = waveletFilterCoefficientsDaubechies16;
const auto &kernelData = kernel.data();
const auto kernelLength = static_cast<int>(kernel.size());

// Precalculated result of the convolution as a reference
const auto &reference = convolutionReferenceResultOfRandomSize32WithDaubechies16;

void directlyDerivedFromEquation(const float *const input, const int inputLength, const float *const kernel, const int kernelLength, float *const output)
{
  const auto outSize = inputLength + kernelLength - 1;
  for (auto outIndex = 0; outIndex < outSize; ++outIndex)
  {
    for (auto inputIndex = 0; inputIndex < inputLength; ++inputIndex)
    {
      const auto kernelIndex = outIndex - inputIndex;
      if ((kernelIndex >= 0) && (kernelIndex < kernelLength)) {
        output[outIndex] += (input[inputIndex] * kernel[kernelIndex]);
      }
    }
  }
}

void directlyDerivedFromEquationWithIfInOuterLoop(const float *const input, const int inputLength, const float *const kernel, const int kernelLength, float *const output)
{
  const auto outSize = inputLength + kernelLength - 1;
  for (auto outIndex = 0; outIndex < outSize; ++outIndex)
  {
    const auto outIndexPlusOne = outIndex + 1;
    const auto inputMin = (outIndexPlusOne >= kernelLength)? outIndexPlusOne - (kernelLength) : 0;
    const auto inputMax = (outIndexPlusOne < inputLength)? outIndexPlusOne: inputLength;
    for (auto inputIndex = inputMin; inputIndex < inputMax; ++inputIndex)
    {
      const auto kernelIndex = outIndex - inputIndex;
      output[outIndex] += (input[inputIndex] * kernel[kernelIndex]);
    }
  }
}

void kernelPerInputValueTransposed(const float *const input, const int inputLength, const float *const kernel, const int kernelLength, float *const output)
{
    for (auto inputIndex = 0; inputIndex < inputLength; ++inputIndex)
    {
        // Makes it obvious for the compiler (especially MSVC) that the factor is constant.
        // Otherwise this message occurs: "1203: Loop body includes on-contiguous accesses into an array".
        const auto inputValue = input[inputIndex];

        for (auto kernelIndex = 0; kernelIndex < kernelLength; ++kernelIndex)
        {
            // It seems to be beneficial to put the constant factor last when MSVC compile option "/fp:fast" is activated.
            output[inputIndex + kernelIndex] += kernel[kernelIndex] * inputValue;
        }
    }
}

void inputPerKernelValueTransposed(const float *const input, const int inputLength, const float *const kernel, const int kernelLength, float *const output)
{
    for (auto kernelIndex = 0; kernelIndex < kernelLength; ++kernelIndex)
    {
        // Makes it obvious for the compiler (especially MSVC) that the factor is constant.
        // Otherwise this message occurs: "1203: Loop body includes on-contiguous accesses into an array".
        const auto kernelValue = kernel[kernelIndex];

        for (auto inputIndex = 0; inputIndex < inputLength; ++inputIndex)
        {
            // It seems to be beneficial to put the constant factor last when MSVC compile option "/fp:fast" is activated.
            output[inputIndex + kernelIndex] += input[inputIndex] * kernelValue;
        }
    }
}

TEST_CASE("directlyDerivedFromEquation is correct", "[convolution]") {
    const auto outputSize = input.size() + kernel.size() - 1;
    std::vector<float> output(outputSize);
    const auto &outputData = output.data();

    directlyDerivedFromEquation(inputData, inputLength, kernelData, kernelLength, outputData);
    REQUIRE_THAT(output, Catch::Matchers::Approx(reference));
}

TEST_CASE("directlyDerivedFromEquationWithIfInOuterLoop is correct", "[convolution]") {
    const auto outputSize = input.size() + kernel.size() - 1;
    std::vector<float> output(outputSize);
    const auto &outputData = output.data();

    directlyDerivedFromEquationWithIfInOuterLoop(inputData, inputLength, kernelData, kernelLength, outputData);
    REQUIRE_THAT(output, Catch::Matchers::Approx(reference));
}

TEST_CASE("kernelPerInputValueTransposed is correct", "[convolution]") {
    const auto outputSize = input.size() + kernel.size() - 1;
    std::vector<float> output(outputSize);
    const auto &outputData = output.data();

    kernelPerInputValueTransposed(inputData, inputLength, kernelData, kernelLength, outputData);
    REQUIRE_THAT(output, Catch::Matchers::Approx(reference));
}

TEST_CASE("inputPerKernelValueTransposed is correct", "[convolution]") {
    const auto outputSize = input.size() + kernel.size() - 1;
    std::vector<float> output(outputSize);
    const auto &outputData = output.data();

    inputPerKernelValueTransposed(inputData, inputLength, kernelData, kernelLength, outputData);
    REQUIRE_THAT(output, Catch::Matchers::Approx(reference));
}

Most Efficient and Maintainable Implementation

After the refinement of the loop order, the following code snipped summarizes the fastest yet simple Convolution implementation of this article:

void convolute(const float *const input, const int inputLength, const float *const kernel, const int kernelLength, float *const output)
{
    for (auto kernelIndex = 0; kernelIndex < kernelLength; ++kernelIndex)
    {
        // Makes it obvious for the compiler (especially MSVC) that the factor is constant.
        // Otherwise this message occurs: "1203: Loop body includes on-contiguous accesses into an array".
        const auto kernelValue = kernel[kernelIndex];

        for (auto inputIndex = 0; inputIndex < inputLength; ++inputIndex)
        {
            // It seems to be beneficial to put the constant factor last when MSVC compile option "/fp:fast" is activated.
            output[inputIndex + kernelIndex] += input[inputIndex] * kernelValue;
        }
    }
}

Features

• Easy to read
• No additional dependencies
• Utilizes auto vectorization capabilities of widely used compilers
• Tested with GCC, CLang and MSVC
• CPU instruction set independent
• No code change for future CPUs

Further Speed Potential

The main idea behind this article is to show how to implement Convolution that is easy to maintain and yet fast. But how much faster can it be made if high maintainability isn’t a key requirement?

As these benchmark charts show, an optimization for AVX using Intrinsics can lead to a solution that is about twice as fast. So there is plenty of potential, if speed is key. But the charts also show, that this optimization is especially significant for AVX CPUs. For new CPUs that support AVX-512, the AVX specific solution still works, but has no significant performance benefit any more. You would need to add AVX-512 specific code for those CPUs to improve speed. ARM CPUs use Neon for vectorization and won’t run with AVX instructions.

There are libraries that provide an abstraction for CPU dependent vector operations, which mitigates that. But these lead to an additional dependency and an abstraction with it’s implied complexity. New CPUs will take some time to get supported by that library, and this would only be the case if it gets maintained frequently.

This is why it is possible to get into the paradox situation where high maintainability beats hand optimized code, just because it is just a matter of a recompile to support a new CPU as soon as the compiler supports it and no additional coding effort or waiting for an update is necessary.

A good hybrid solution could be a manually optimized solution for hardware, that is used by the majority of users as well as a fallback to the solution shown here in other cases.

Source Code

The source code can be found on GitHub in the repository JohT/convolution-benchmarks [4]. It contains:

• The previously described implementation variations in JohTConvolution.h
• Some other implementations
• Fully automated Unit Tests
• Fully automated micro benchmarks with visualized reports as described in Visualize Catch2 benchmarks with Vega-Lite [5]

---

References

• [1] Intuitive Guide to Convolution (Kalid Azad)
  https://betterexplained.com/articles/intuitive-convolution
• [2] The Convolution Series (Jan Wilcze)
  https://thewolfsound.com/convolution-the-secret-behind-filtering
• [3] ISO/IEC 9126
  https://www.iso.org/standard/22749.html
• [4] convolution-benchmarks (GitHub)
  https://github.com/JohT/convolution-benchmarks
• [5] Visualize Catch2 benchmarks with Vega-Lite
  https://joht.github.io/johtizen/data/2022/09/05/visualize-catch2-benchmarks-with-vega-lite.html
• [6] Branchless Programming
  https://dev.to/jobinrjohnson/branchless-programming-does-it-really-matter-20j4
• [7] Quick C++ Benchmark
  https://quick-bench.com
• [8] Godbolt Compiler Explorer
  https://godbolt.org
• [9] Clang Compiler
  lang.llvm.org
• [10] Intel® Intrinsics Guide
  https://www.intel.com/content/www/us/en/docs/intrinsics-guide/index.html
• [11] Pipelined Direct Form FIR Versus the Transposed Structure
  https://www.allaboutcircuits.com/technical-articles/pipelined-direct-form-fir-versus-the-transposed-structure
• [12] Microsoft Visual Studio C++ Compiler (MSVC)
  https://visualstudio.microsoft.com/de/vs/features/cplusplus
• [13] MSVC Auto-Vectorizer Reporting Level
  https://docs.microsoft.com/en-us/cpp/build/reference/qvec-report-auto-vectorizer-reporting-level
• [14] MSVC Auto-Parallelization and Auto-Vectorization
  https://docs.microsoft.com/en-us/cpp/parallel/auto-parallelization-and-auto-vectorization
• [15] GNU GCC Compiler
  https://gcc.gnu.org
• [16] Catch2
  https://github.com/catchorg/Catch2
• [17] Dirac delta (Wikipedia)
  https://en.wikipedia.org/wiki/Dirac_delta_function
• [18] Kronecker delta (Wikipedia)
  https://en.wikipedia.org/wiki/Kronecker_delta#Digital_signal_processing

---

Hint: If you want to reach out to me without leaving a comment below, open a new discussion on GitHub.